Esquema de los Números Reales: Guía Completa y Visual para Entender su Estructura
Introducción a los Números Reales
¿Alguna vez te has preguntado qué son realmente los números reales? A menudo, escuchamos términos como «números enteros», «números racionales» y «números irracionales», pero ¿cómo encajan todos estos en un solo concepto? En este artículo, vamos a desglosar el vasto mundo de los números reales. Prepárate para un viaje que te ayudará a entender no solo la definición, sino también la estructura y la importancia de los números reales en matemáticas y en la vida diaria.
¿Qué Son los Números Reales?
Los números reales son, en esencia, todos los números que puedes encontrar en la recta numérica. Desde los enteros, como -2, 0 y 3, hasta los números decimales, como 3.14 y -0.5, todos ellos son parte de este conjunto. Pero eso no es todo; también incluye números que no pueden expresarse como fracciones, como √2 o π. Así que, en resumen, los números reales son un gran paraguas que cubre una variedad de tipos de números.
La Recta Numérica: Un Vistazo Visual
Imagina la recta numérica como una línea infinita que se extiende en ambas direcciones. En el centro, tienes el 0, y a la derecha, los números positivos van aumentando, mientras que a la izquierda, los números negativos disminuyen. Cada punto en esta línea representa un número real. Es como un mapa donde cada destino es un número, y puedes moverte a lo largo de la línea para encontrar cualquier número real que desees. ¡Sencillo, verdad?
Clasificación de los Números Reales
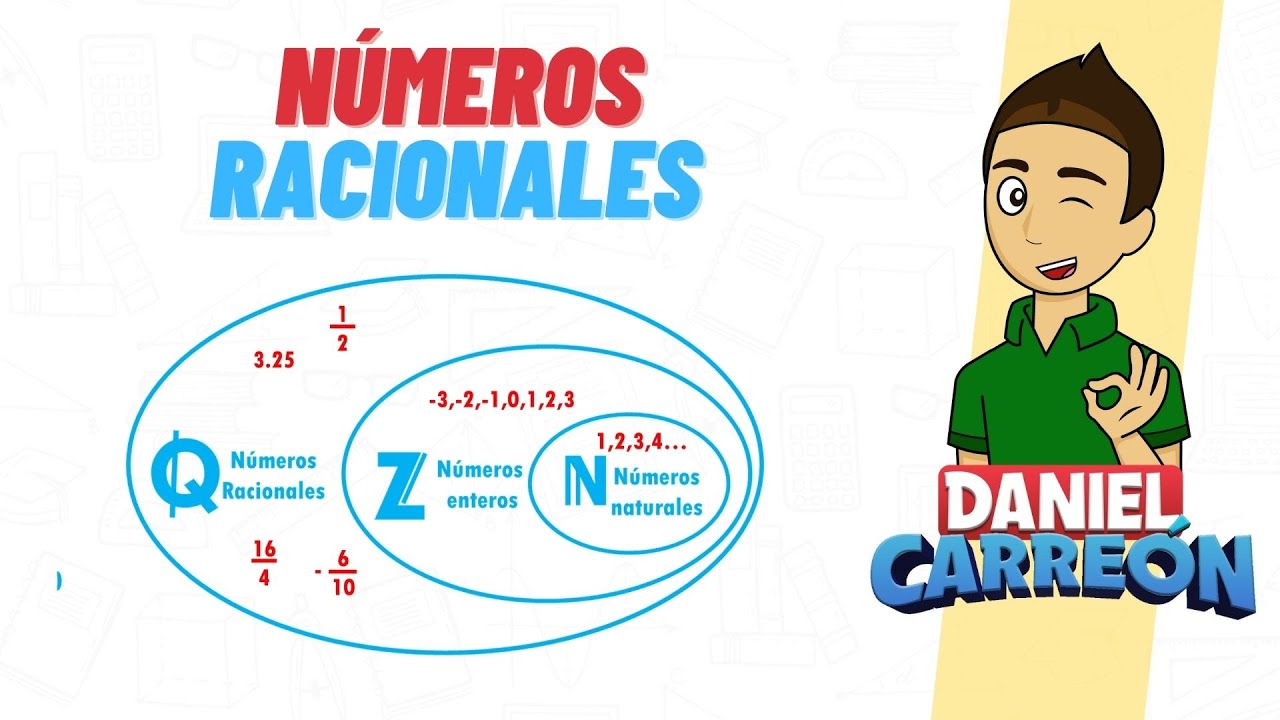
Ahora que tenemos una idea básica de qué son los números reales, vamos a clasificarlos. Esta clasificación es fundamental para entender su estructura. Los números reales se dividen en dos categorías principales: números racionales e irracionales.
Números Racionales
Los números racionales son aquellos que se pueden expresar como el cociente de dos enteros. En otras palabras, si puedes escribir un número en la forma a/b, donde a y b son enteros y b no es cero, entonces tienes un número racional. Ejemplos incluyen 1/2, -3, y 0.75. Puedes pensar en los números racionales como los «números amigables» que pueden ser divididos y compartidos fácilmente.
Números Irracionales
Por otro lado, los números irracionales no pueden ser expresados como el cociente de dos enteros. Esto significa que tienen decimales que nunca terminan y nunca se repiten. Algunos ejemplos famosos son √2 y π. Imagina que estás en una fiesta y todos los números racionales están charlando y compartiendo historias, mientras que los números irracionales están en un rincón, disfrutando de su propia conversación infinita. ¡No hay manera de que se integren!
Propiedades de los Números Reales
Los números reales tienen varias propiedades interesantes que son fundamentales en matemáticas. Vamos a explorarlas un poco más.
Cerradura
La propiedad de cerradura significa que cuando realizas una operación (suma, resta, multiplicación o división) con dos números reales, el resultado también será un número real. Es como un club exclusivo: una vez que entras, todos los que estén dentro también son parte del club.
Conmutativa y Asociativa
Las propiedades conmutativa y asociativa son como las reglas de un juego. La propiedad conmutativa dice que puedes cambiar el orden de los números en una operación sin afectar el resultado. Por ejemplo, 2 + 3 es lo mismo que 3 + 2. Por otro lado, la propiedad asociativa te permite agrupar los números de diferentes maneras. Por ejemplo, (2 + 3) + 4 es lo mismo que 2 + (3 + 4). ¡Es como tener la flexibilidad de reordenar tus muebles sin que se vea diferente!
Identidad
La propiedad de identidad establece que hay ciertos números que, al sumarse o multiplicarse, no alteran el valor de otro número. En el caso de la suma, el número 0 es el elemento neutro, y para la multiplicación, es el 1. Puedes pensar en ellos como los «números silenciosos» que no hacen ruido cuando se les añade o multiplica.
La Importancia de los Números Reales
Ahora que hemos cubierto qué son y cómo se clasifican los números reales, es esencial entender por qué son importantes. Los números reales son la base de muchas áreas de las matemáticas y tienen aplicaciones en la vida cotidiana.
Aplicaciones en la Vida Real
Imagina que estás cocinando y necesitas medir ingredientes. Los números reales te permiten medir con precisión, ya sea que uses 1.5 tazas de harina o 0.75 litros de leche. Sin los números reales, la cocina sería un caos. Además, los números reales son fundamentales en campos como la física, la ingeniería y la economía, donde las mediciones precisas son cruciales.
Fundamento de Otras Matemáticas
Los números reales también son la base para otros conceptos matemáticos más avanzados. Por ejemplo, en cálculo, los límites y las funciones se basan en números reales. Sin ellos, no podríamos avanzar a conceptos más complejos. Es como construir una casa: los números reales son los cimientos que sostienen todo el edificio.
Conclusión
Los números reales son un concepto fascinante y fundamental en matemáticas. Desde su clasificación en racionales e irracionales hasta sus propiedades y aplicaciones en la vida diaria, hemos visto que son mucho más que simples números en una línea. Así que la próxima vez que veas un número, recuerda que detrás de él hay un mundo completo de ideas y conceptos. ¿Te has preguntado alguna vez cómo se relacionan los números reales con otros campos del conocimiento? ¿O cómo afectan tu vida diaria más de lo que piensas?
Preguntas Frecuentes
1. ¿Los números reales son infinitos?
¡Sí! Los números reales son infinitos. Hay una cantidad infinita de números entre cualquier par de números reales. Por ejemplo, entre 1 y 2, puedes encontrar 1.1, 1.01, 1.001, y así sucesivamente.
2. ¿Cuál es la diferencia entre números racionales e irracionales?
La diferencia principal es que los números racionales pueden expresarse como fracciones de enteros, mientras que los números irracionales no pueden. Por ejemplo, 1/2 es racional, pero √2 es irracional.
3. ¿Por qué son importantes los números reales en matemáticas?
Los números reales son fundamentales porque forman la base de muchas áreas de las matemáticas, incluyendo álgebra, geometría y cálculo. Son esenciales para entender conceptos más complejos.
4. ¿Cómo se utilizan los números reales en la vida diaria?
Los números reales se utilizan en diversas situaciones cotidianas, como medir ingredientes al cocinar, calcular distancias en viajes o manejar finanzas personales. ¡Son más útiles de lo que parece!
5. ¿Pueden los números reales ser negativos?
Sí, los números reales incluyen tanto números positivos como negativos. En la recta numérica, los números negativos se encuentran a la izquierda del 0.